Коротко: Коэффициент вариации, VAR или CV, — ключевой показатель в оценке риска проектов и доходности ценных бумаг. Он позволяет заранее проанализировать сразу два показателя, которые обладают меняющимися во времени значениями. Если показатель оказывается менее 0,1, направление инвестирования характеризуется низким уровнем риска. При показателе свыше 0,3 уровень риска необоснованно высок. Для расчета удобнее всего использовать функции СТАНДОТКЛОН и СРЗНАЧ табличного редактора Excel.
Подробно
Для того чтобы сформировать качественный инвестиционный портфель, инвесторам порой приходится прибегать к оценке входящих в него активов, которые обладают разным уровнем риска и доходности. Для этой цели используется широко известный в инвестиционном анализе и эконометрике показатель.
Коэффициент вариации (Coefficient of variation — CV, VAR) — относительный финансовый показатель, который демонстрирует сравнение рассеивания значений двух случайных показателей, которые имеют разные единицы измерения относительно ожидаемого значения.
Справка! Поскольку коэффициент вариации позволяет получить сопоставимые результаты, то его применение оптимально в рамках портфельного анализа. В ней он позволяет эффективно объединить значения риска и доходности и вывести результирующее значение.
Coefficient of variation — показатель из числа относительных методов статистики, который, как NPV и IRR, применяется в рамках инвестиционного анализа. Он измеряется в процентах и может применяться для сравнения вариаций двух несвязанных между собой критериев. Его чаще всего используют финансовые и инвестиционные аналитики.
Справка! На базе коэффициента вариации оценивается так называемый «унифицированный риск» (unitized risk), поскольку он оценивает относительный разброс двух показателей по отношению к прогнозному значению.
Для чего используют показатель VAR:
- в целях сравнения двух разных показателей;
- для определения степени устойчивости прогнозных моделей (в основном по инвестициям и портфельному инвестированию);
- для осуществления XYZ-анализа.
Справка! XYZ-анализ — аналитический инструмент, в рамках которого продукция компании оценивается по двум параметрам: стабильность потребления и продаж.
Формула расчета коэффициента вариации
Суть расчета коэффициента вариации состоит в том, что по множеству значений рассчитывается сначала среднее квадратичное отклонение, а затем — среднее арифметическое, а после — найти их соотношение.
В общем виде формула расчета показателя VAR выглядит следующим образом:
CV = σ / t ср, где:
CV — коэффициент вариации;
σ — среднее квадратическое отклонение;
t — среднее арифметическое значение для случайной величины.
Формула расчета показателя VAR может принимать самые разнообразные интерпретации в зависимости от объекта оценки.
Важный момент! Очевидно, что применение представленных выше формул вручную, в особенности при наличии широкого круга значений, весьма затруднительно. Оттого для расчета применяется инструментарий табличного редактора Excel.
Значения показателя VAR в инвестиционном анализе
CV — показатель, который можно считать более универсальным, чем дисперсия или среднее квадратичное отклонение: на его основе можно сопоставлять риски и доходности двух и более активов, существенно отличающихся друг от друга.
Нормативного значения этого показателя не существует. Однако имеются некоторые опорные критерии, которые помогают при его анализе и интерпретации.
Важный момент! Коэффициент CV имеет несколько недостатков — он не учитывает величины первоначальных вложений, предполагает симметричность разбросанных значений по отношению к среднему, а также не может использоваться для опционов, доходность которых может быть меньше 0. Оттого при наличии сомнений стоит дополнительно использовать показатели IRR и NPV.
Примеры расчета VAR в Excel
Расчет коэффициента вариации вручную − сложная и затяжная по времени процедура. Если выборка значительная, то расчёт по ней среднего квадратического отклонения вручную крайне чреват ошибками и неточностями.
Удобный способ определения VAR предлагает табличный редактор Excel. На его базе можно рассчитать:
- среднее квадратическое отклонение (функция СТАНДОТКЛОН);
- среднее арифметическое (функция СРЗНАЧ).
Для того чтобы разобраться в тонкостях использования CV, имеет смысл привести пример его расчета.
Пример расчета: оценка двух проектов с разной прибылью
Существует два бизнеса, которые на протяжении 5 лет демонстрируют разный финансовый результат. Для того чтобы сделать выбор между ними, инвестору стоит рассчитать коэффициент вариации.
Первоначально рассчитаем среднее квадратичное отклонение, используя статистическую функцию Excel СТАНДОТКЛОН.В.
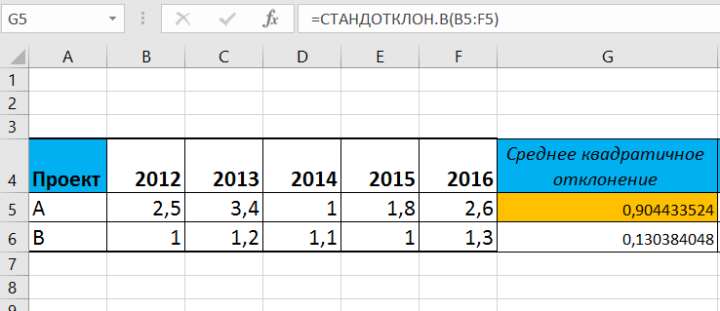
Рисунок 1. Расчет среднего квадратического отклонения по проекту А.
Аналогичным образом на базе статистической функции СРЗНАЧ рассчитывается среднее арифметическое по обоим проектам
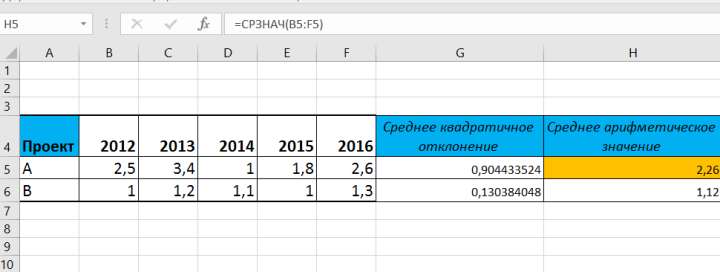
Рисунок 2. Расчет среднего арифметического значения по проекту А.
После этого остается разделить среднее квадратическое отклонение на среднее арифметическое и получить результат — значение коэффициента вариации.
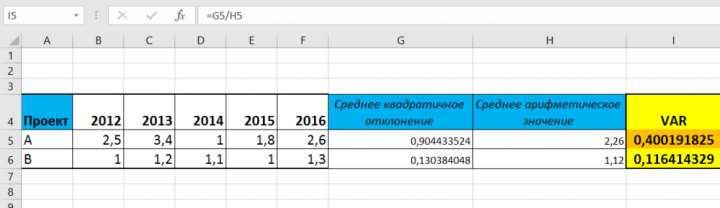
Рисунок 3. Расчет VAR по проекту А.
Вывод! По проекту А уровень риска оказался равным 40%. При таком раскладе он представляется рискованным и неустойчивым. По проекту В уровень риска приемлемый — всего 11,64%. Инвестору уместно вложить средства в более надежный проект В, хотя в отдельные периоды проект А приносит большую прибыль.
Детальный алгоритм расчета показателя представлен в образце, составленном на базе табличного редактора Excel.
Детальный процесс расчета показателя вариации представлен в видеоролике.