Условная функция и логические выражения в электронной таблице Excel
- Трофимова Вера Владимировна, зам. директора по УВР, учитель информатики
Разделы: Информатика
В соответствии с программой по информатике тема «Технология обработки числовой информации» изучается в курсе основной школы, а более углубленно — в курсе средней школы. Материалы для изучения этой темы в основной школе я уже представляла на Фестивале «Открытый урок» (см. мои материалы по теме «Изучаем табличный процессор Excel в 8 класс»). В старшей школе после изучения темы «Логические величины и логические операции» можно провести урок по теме «Технология обработки числовой информации» с опорой на знание логических операций.
1. Создание проблемной ситуации
Ученики сдают зачет, который предусматривает систему оценивания «зачет» и «незачет». «Зачет» ставится, если из 10 вопросов ученики верно ответили больше чем на половину вопросов, т.е. на 6 и более, а в противном случае ставится «незачет». Надо автоматизировать процесс выставления зачета.
Давайте подумаем, какую информацию надо занести в электронные таблицы, какие задать формулы?
После обсуждения с учениками останавливаемся на таблице следующего вида:
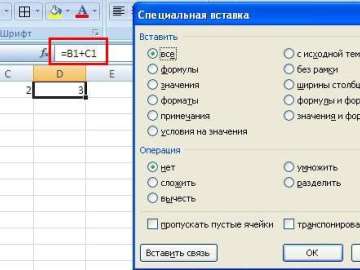
В ячейки А2:К6 заносим данные (1 — верный ответ, 0 — неверный), а в ячейки L2:М6 заносим формулы. В ячейке L2 будет формула =СУММ (В2:К2). Эту формулу надо скопировать в другие ячейки столбца L (по количеству учеников).
Какую формулу надо задать в ячейке М2?
Создана проблемная ситуация, для преодоления которой ученикам необходимы новые знания.
2. Изучение нового материала (ведется с использованием презентации)
Слайд 1. Общий вид условной функции.
Условная функция, записанная в ячейку таблицы, выполняется так: если условие истинно, то значение данной ячейки определяется значением <выражения 1>, в противном случае — значением <выражения 2>.
Слайд 2. Построение логических выражений
Логические выражения строятся с помощью операций отношения (<,>, <=, >=, <>) и логических операций (логическое И, логическое ИЛИ, логическое отрицание НЕ). Результатом вычисления логического выражения являются логические величины ИСТИНА или ЛОЖЬ.
Слайд 3. Особенности логических операций в электронных таблицах.
Слайд 4.Есть ли действительные корни у квадратного уравнения
Даны коэффициенты а, b, c квадратного уравнения (а?0). Определить, имеет ли это уравнение действительные корни
Решение. Исходной информацией являются коэффициенты а, b, c. Готовим таблицу в следующем виде:
В ячейки А2:С2 заносим числовые значения коэффициентов.
В ячейку D2 заносим формулу для вычисления дискриминанта квадратного уравнения =В^2-4*A2*C2. В ячейку Е2 заносим формулу =ЕСЛИ (D2>=0; «ДА»; «НЕТ»). Таким образом, если условие D2>=0 (то есть если дискриминант неотрицателен), то в ячейке Е2 будет отражаться текст «ДА», противном случае — «НЕТ».
Приведенный пример (слайд 4) разбирает учитель. Следующий пример (слайд 5) ученики должны объяснить самостоятельно.
Слайд 5. Принадлежность точки прямой
Даны коэффициенты k, b уравнения прямой у= kх+ b и даны координаты (х,у) пяти точек на плоскости. Для каждой точки определить, принадлежит ли она данной прямой или нет.
Решение. Если точка принадлежит прямой, то при подстановке координат точки в уравнение этой прямой получается верное равенство. Готовим таблицу в следующем виде:
В ячейки А2,В2, заносим численные значения коэффициентов k, b. В ячейки С2:С6, D2: D6 заносим соответствующие координаты пяти точек. В ячейку Е2 заносим формулу = ЕСЛИ($A$2*C2+ $B$2=D2; «ДА»; «НЕТ»). Далее копируем эту формулу для ячеек Е3:Е6. Таким образом, если условие у= kх+ b выполняется для данной точки с координатами (х,у), то в соответствующей ячейке столбца Е будет отражаться текст «ДА», в противном случае — «НЕТ». В ходе решения этой задачи с учениками необходимо обратить внимание на то, почему использованы абсолютные ссылки на ячейки А2 и В2.
Следующий, более сложный, пример (слайд 6) учитель разбирает подробно.
Слайд 6. Принадлежность точки прямоугольнику.
Даны координаты вершин прямоугольника (х1,у1), (х1,у2), (х2,у2), (х2,у1), расположенного в первом квадранте, со сторонами, параллельными осям координат (0 < х1 < х2, 0 < у1 < у2), и даны координаты точки (х,у). Определить, лежит ли эта точка внутри прямоугольника (включая его границы) или нет.
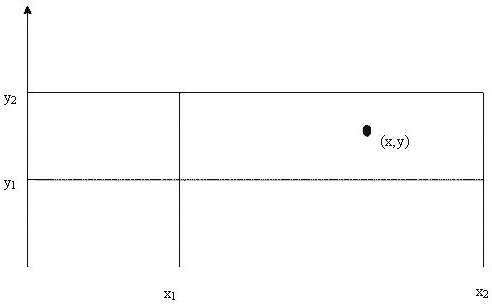
Решение. Если точка с координатами (х,у) лежит внутри прямоугольника или на его границе, то должны выполняться следующие условия:
. (1)
Готовим таблицу в следующем виде:
В ячейки А2: F2 заносим соответствующие данные. В ячейку G2 заносим формулу: =ЕСЛИ (И (Е2>=$A$2; E2<=$B$2; F2>=$C$2; F2<=$D$2); «Да»; «Нет»).
Здесь нам пришлось использовать логическое выражение (1) и учесть особенности записи логических операций в табличных процессорах.
При занесении формулы в ячейку G2 мы встретимся с ситуацией, когда при вставке встроенной функции ЕСЛИ требуется в качестве её аргумента указать другую встроенную функцию И. Выясним, как это сделать. Вызываем мастер функций, выбираем функцию ЕСЛИ. Вводим значение «Да» в поле «Значение_если_истина», вводим значение «Нет» в поле «Значение_если_ложь». Устанавливаем курсор в поле «Логическое выражение» и вставляем это поле логическую функции И, но не с помощью панели инструментов, а через дополнительный список слева вверху. Далее заполняем соответствующие поля ввода для логической функции И.
Теперь вернемся к ситуации, поставленной в начале урока.
Слайд 7. Так как же записать формулу в ячейке М2?
3.Этап закрепления знаний
Далее предлагается задача для самостоятельного решения учащимися (фронтальная работа)
Слайд 8. Подсчет стоимости телефонных переговоров
Решение. Используем заранее подготовленную таблицу стоимости телефонных переговоров.
Если звонок производится по льготному тарифу, то должно выполняться условие: День недели = «суббота» ИЛИ День недели = «воскресенье» ИЛИ Праздник «Да» ИЛИ время начала переговоров >=20 ИЛИ Время начала переговоров <=8. Поэтому в ячейку G3 заносим формулу: ЕСЛИ (ИЛИ (С3= «Суббота»; С3= «Воскресенье»; D3= «Да»; Е3>=20; Е3<=8);$D$1*F3; $B$1*F3).
Ссылка на ячейки D1 и В1 абсолютная, так как при копировании формул имена этих ячеек не должны меняться.
При решении этой задачи закрепляются умения учащихся записывать логические выражения в табличных процессорах; использовать вложенные функции.
Для проверки решения учащимся демонстрируется заранее подготовленный файл с результатами решения:
4. Самостоятельная работа учащихся
Задача 2 (уровень 2). Покупатель магазина получает скидку 3%, если у него есть дисконтная карта или если общая стоимость его покупки превышает 5 тысяч рублей. Определить, сколько заплатили покупатели за свои покупки с учетом дисконта (если он есть).
Задача 3 (уровень 3). Торговый склад производит уценку хранящейся продукции. Если продукция хранится на складе дольше 10 месяцев, то она уценивается в 2 раза, а если срок хранения превысил месяцев, но не достиг 10 месяцев — то в 1,5 раза. Получить ведомость уценки товара, которая должна включать следующую информацию: наименование товара, срок хранения, цена товара до уценки, цена товара после уценки.
5. Домашнее задание
Подготовлены задания трех уровней сложности, каждому ученику выдается карточка.
Задача 1 (уровень 1). Компания по снабжению электроэнергией взимает плату с клиентов по тарифу: 0,6 рублей за 1 кВт/ч за первые 200 кВт; 0,9 рублей за 1 кВт/ч, если потребление свыше 200 кВт. Услугами компании пользуются 10 клиентов. Подсчитать плату для каждого клиента.
Задача 2 (уровень 2). Компания по снабжению электроэнергией взимает плату с клиентов по тарифу: 0,6 рублей за 1 кВт/ч за первые 200 кВт; 0,9 рублей за 1 кВт/ч, если потребление свыше 200 кВт, но не превышает 500 кВт; 1,2 рубля за 1 кВт/ч, если потребление свыше 500 кВт. Услугами компании пользуются 10 клиентов. Подсчитать плату для каждого клиента.
Задача 3 (уровень 3). К задачам предыдущего уровня сложности добавляются следующие задания: подсчитать суммарную плату всех клиентов, определить, сколько клиентов потребляет свыше 500 квт.